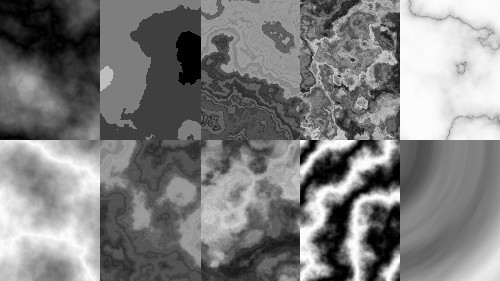
10 Noise Transformations

An exploration into interesting transformations of noise*.

*Noise as a term is very broad. In this case I am using what is often referred to as Fractional Brownian Motion, or Octaved Perlin Noise. It produces cloud-like textures when using the output as the “brightness” of a pixel:

Some useful resources for those who are unfamiliar:

• Adrian Biagioli has a Perlin Noise write up which explains how Perlin Noise works, but more importantly how to build Octaved Perlin Noise
• Book of Shaders is a great resource and describes some of these ideas
• There are a few variations on Perlin noise, case in point I am actually using an implementation OpenSimplex which has some benefits over the original Perlin noise, but for the most part the results would be fairly similar regardless of the implementation you use

In the rest of the post for simplicity noise(x,y) is a function which outputs a noise value in the range [-1,1] based on an input x and y value (e.g. co-ordinates of pixels on your canvas). It’s worth checking first the output range of your own noise function, as some are normalised to [0,1] out of the box.

Let’s get stuck in…

1. Valleys

Starting fairly simple, by taking the absolute value of noise, the output will have harsh, dark creases that look like valleys. Note that taking the absolute value will change the output range from [-1,1] to [0,1], so you may need to adjust how you convert the value to a colour.

func valleyNoise(x float64, y float64) float64 {
    return math.Abs(noise(x, y))
}

2. Ridges

A simple extension to this is to invert the noise so the valleys become ridges. This gives more of a “lightning” like look

func ridgeNoise(x float64, y float64) float64 {
    return 1-math.Abs(noise(x, y))
}

3. Stepped

By using a floor-function to round down noise values, the result looks more like islands or continents. Depending on the value that you multiply/divide by, you will get more discrete “levels”

A more extreme version of this would be to replace the floor-function with an if statement, returning 1 above a certain threshold and 0 otherwise. Then the threshold could be adjusted lower to produce large continents or higher to produce smaller islands in large oceans.

func steppedNoise(x float64, y float64) float64 {
    return return math.Floor(noise(x, y)*2) / 2
}

4-7. Noise Warp

The next few examples are partially inspired by Inigo Quilez’s Warp post, though less rigorous and more basic!

First, I tried using noise within noise. This created an interesting texture where the contours seemed to be subtlely emphasised, leading to ridges that form circuits (note that the inner noise had to be scaled to a sensible effect, and I also added a small shift to the secondary x,y values - I imagine there’s more mileage to be found in playing with these parameters). I also scaled the resulting noise as it was a little muted.

func warpANoise(x, y float64) float64 {
    return noise(1+noise(x, y)*200, 2+noise(x, y)*200) / 0.8
}

Second, I added yet another noise on top in the same manner. This led to a slightly altered effect with additional contours. In some respects the pattern reminds me of an oil slick.

func warpBNoise(x, y float64) float64 {
    n2 := func(x, y float64) float64 {
        return noise(1+noise(x, y)*200, 2+noise(x, y)*200) / 0.8
    }
    return noise(1+n2(x, y)*200, 2+n2(x, y)*200) / 0.8
}

Third, I went back to the original warped noise and altered it so that the inner noise had different parameters by offsetting x and y on one of them (comparing the code for both will probably be clearer than trying to explain it in words!). This resulted in an effect that looks more like a fuzzy fabric of some kind, or short fur.

func warpCNoise(x, y float64) float64 {
    return noise(1+noise(x, y)*200, 2+noise(10+x, 20+y)*200) / 0.8
}

Finally, I combined the ideas of B and C by adding an offset to the triple noise. The output of this reminded me of granite, with patterns you might see in a stone kitchen worktop.

func warpDNoise(x, y float64) float64 {
    n2 := func(x, y float64) float64 {
        return noise(1+noise(x, y)*200, 2+noise(10+x, 20+y)*200) / 0.8
    }
    return noise(1+n2(x, y)*200, 2+n2(50+x, 20+y)*200) / 0.8
}

8. Stripes

Now taking a different tack, I introduced a Sine wave into the mix. Sine(x + y) produces a black and white striped gradient. By adding a turbulence in the form of noise Sine(x + y + noise(x,y)*turbulence) the stripes become distorted, with the turbulence parameter as a way to control the amount of distortion.

func stripedNoise(x, y float64) float64 {
	return math.Sin((x+y)/10 + 10*noise(x, y))
}

9. Marble

Playing around with the previous example, it’s possible to produce something approximating a marble texture. I re-used the absolute value trick from the first example, followed by using power function to change the dynamics of the output. This could almost certainly be improved upon to be more realistic, but this result in itself is fairly interesting.

func stripedNoise(x, y float64) float64 {
	xy := x + y + (1+noise(x,y))
	return math.Pow(math.Abs(math.Sin(xy*math.Pi)),0.1)
}

10. Polar Noise

In the past I have found I had need of a noise function similar to Fractional Brownian Motion but that can be referenced seamlessly in polar co-ordinates (e.g. by radius and angle instead of x and y). Just blindly using the same noise function with radius and angle in place of x and y will lead to an ugly artifact where 360 degrees meets 0 degrees. A solution that worked quite well for me was to use Sine(angle) in place of the angle, since the value of this will be same at both 0 and 360 degrees. I also multiply this by the radius so that the angle noise scales accordingly with radius. You can play with different scaling factors on both arguments to noise(x,y) to achieve different effects.

func polarNoise(rad, ang float64) float64 {
	return noise(rad, math.Sin(ang)*rad/5)/0.8
}